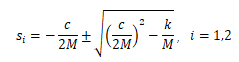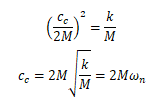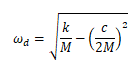03 | 有阻尼单自由度系统-压力管道振动分析

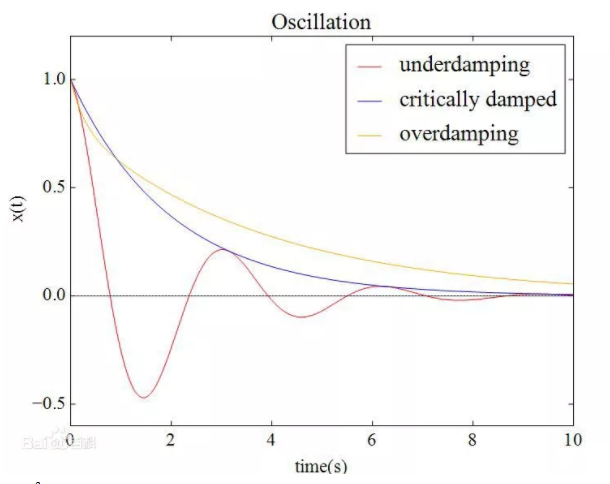
01-有阻尼单自由度系统

阻尼是阻止结构发生变形的载荷，它会减少系统的响应。因此，在动态分析里面如果忽略掉阻尼，是一种保守的做法。因为没有阻尼我们得到的响应会更大。这是不太经济的一种设计方法。阻尼大致可分为两类，一类叫粘性阻尼，这类阻尼跟结构参与部分的速度成比例关系。主要由结构内部的粘滞性及阻止结构发生变形的一些因素组成。另一类叫库伦阻尼，跟结构摩擦力相关，比如支架的摩擦力。通常把库伦阻尼近似的放进黏性阻尼里面进行考虑。接下来我们详细的讨论一下在阻尼存在的情况下，结构的振动分析。

有阻尼的结构振动方程如下式：

(a)     黏性阻尼系统的自由振动。在无阻尼系统里面，给一个很小的位移扰动，系统将会以相同的振幅持续的振动下去。但是在阻尼系统里面，这个振幅会很快的衰减下来。要研究阻尼系统的固有频率，设置外载荷为0，得到下面的振动方程：

设置并代入上式来求解这个线微分方程，得到：

上面一元二次方程的根为：

通解为：

根据s₁和s₂的不同值，上面的通解会展示出不同的特征。

当时，s₁和s₂是两个实根，但是都是负数，因此代入通解后，你会发现响应y从一开始就是持续衰减的，没有发生振荡。我们称这种情况为过阻尼系统，过阻尼系统在现实的工程结构中几乎没有，因此这里我们就不讨论了。

当时，s₁和s₂是两个重根，称这个情况为临界阻尼状态，这时我们会得到一个非常重要的参数，临界阻尼：

当时，s₁和s₂是一对共轭复数根，为了使解有物理意义，C₁和C₂也应该取一对共轭复数。我们称这种情况为欠阻尼系统。根据初始条件，最终可以将通解化简成下面的形式：

就是这个欠阻尼系统的角频率。

注意是无阻尼系统的角频率。前面我们已经习惯了无阻尼系统的分析，更能让我们接受，那可以根据临界阻尼关系式给建立一种关系。

令，称为阻尼比，这是系统阻尼和临界阻尼的比值。

上面的式子展示了阻尼系统和无阻尼系统的角频率关系。如系统有10%的阻尼比，阻尼系统的角频率。差距很小，这就是为什么我们在实际做结构分析的时候忽略掉阻尼的原因。换个角度说，通常阻尼系统的固有频率是基于无阻尼系统计算而来的。

     根据初始条件，，可以将阻尼系统的自由振动方程通解解出：

   将上式和无阻尼系统自由振动的解做个对比：

   主要结构是一样的，是一个振荡的曲线，只不过前面多了一项，这个指数项很明显会持续衰减振动响应的振幅。

   （b）具有初始位移的黏性阻尼系统自由振动。前面无阻尼系统自由振动分析时我们做过相同的事情，在这儿也一样。我们将模拟的这个结构质量点初始位移放在处，然后释放开，质量点就开始发生自由振动。那么在这个振动过程中，质量点的位移和时间的关系我们就可以通过上面的解得到了。因为是一个常数，所以。

    这个看似复杂的式子其实本身就是一个三角函数曲线，画出的曲线如下图。看上式正弦部分，是十分接近的，而通常是一个非常小的量，那么与比起来就是一个小量了，因此上面的响应值可以把正弦部分忽略掉，这样具有初始位移的黏性阻尼系统自由振动解就可以近似用下面的式子来表达了：

    这个响应是一个余弦函数，幅值是伴随时间被削减的。

    通过上面的曲线可以看到，时间每经过就会出现峰值。跟无阻尼自由振动相比较，峰值是在作用下持续降低的。阻尼比是一个很难确定的值，比如一栋大楼或一个管道系统，要得到它精确的阻尼是很难的一件事情。但是通过这个阻尼振动响应公式，我们能找到一种确定阻尼比的可能性。简单来说，可以通过测量阻尼系统不同周期的振动振幅来计算。具体做法是将第n个波峰与第n+1个波峰相比：

    两边取对数，

    再做一点化简得到只关于的式子，这样我们就可以根据测量的数据直接计算出阻尼比系数了：

    这就是为什么在做建筑结构动态分析的时候，通常会给定阻尼比而不是直接指定阻尼系数c。当然刚才我们计算的是两个相邻波峰的比值，相邻波峰的比值很小，计算起来精度要差一些，通常会测量相邻j个周期的波峰，然后做上面的计算，这样更容易得到阻尼比系数。计算式子如下：

(c)有阻尼单自由度系统振动方程另一种形式。将阻尼比代入振动方程，得到振动方程新的形式：

(d)动载荷作用下的阻尼系统。针外载荷为冲击力的情况，冲击过程十分短暂，从冲击开始到结束，阻尼系统振动可能都不到一个周期，所以，阻尼对冲击载荷的响应影响很小。如果动载荷是简谐载荷，那需要认真去研究它对结构振动特性的影响了。

    上式的自由振动通解我们已经求出来了：

    接下来只需要找到一个特解就可以将简谐载荷情况的振动方程完全求出来。

    设代入振动方程，可求得一个特解：

    最终通解为：

    其中，

  上面的通解包含两部分，加号前面部分为自由振动的贡献，后面部分为简谐载荷的贡献。自由振动部分在阻尼的作用下会很快的被衰减掉，真正体现出来的响应主要是加号后面的部分。因此将自由振动部分忽略掉，得到阻尼系统在简谐载荷作用下的响应方程：

    现在响应方程虽然得到了大大的简化，是一个纯粹包含正余弦的公式，但依然不方便我们做直观的判断，可以进一步化简，接下来做一个正余弦的变换（这纯粹就是玩数学游戏了）：

    所以可以得到，

    准备工作做足一点，

    令，，为相位角，最终可得y的解：

    其中相位角，

    现在很容易知道，当时，y达到最大值，DLF的最大值可以得出：

    将DLF作为纵轴，作为横轴，画出关系曲线如下图。通过图表我们可以获得这些信息：DLF最大值受到两方面影响，阻尼比，和外载荷频率与无阻尼状态结构固有频率之比。

    如果

    外载荷角频率与固有角频率相等，产生共振。如果没有阻尼，=0，DLF趋于无穷大，这就是前面我们说到的无阻尼状态。通常管道系统的阻尼比在2%到8%之间，取决于管道的管径，保温，固有频率等。假设我们的管道系统阻尼比为5%，共振时，DLF为10，也就是说管道系统受到一个很小的振动激励，结构的响应就会放大10倍。

    上面是单自由度系统振动的基础知识，做个小总结：

    单自由度系统的特性分析方法也用到实际工程中，实际的工程结构是多自由度系统。在后面会继续讲到多自由度系统的分析。

（1）       结构系统最基本的特性就是固有频率，固有频率与这个结构刚度质量比成比例关系。刚度很大的结构系统具有较高的固有频率，但是庞大的质量会降低固有频率。

（2）       阻尼对结构的固有频率影响很小，所以在计算结构固有频率时通常忽略掉阻尼。

（3）       冲击载荷作用下，结构的响应大小取决于冲击载荷的作用时长和结构的固有频率大小。冲击时长越短，结构还没来得及响应就结束了。所以冲击载荷造成的DLF最大可以达到2，但是冲击时间越短，DLF也可能接近0。

（4）       结构响应分成两部分：一部分是结构的自由振动，一部分是外载荷作用的振动。在冲击载荷作用的系统中，这两部分响应都非常重要。但是对于外载荷作用时间长的这种简谐载荷或周期性载荷来讲，振动响应最终都只是外载荷引起的这部分保持稳定振动，自由振动这部分影响变小。

（5）       简谐载荷或其它的周期性载荷作用在结构上面时，响应可能会特别大。特别当外载荷的频率接近于结构系统的固有频率时，振动最剧烈。当外载荷频率等于结构固有频率时，响应最大，称为共振。

（6）     具有相同角频率的正弦曲线和余弦曲线组合，得到一个放大的正弦曲线。即，。不同角频率的正弦曲线和余弦曲线组合不会得到纯正的正弦曲线，如下图所示，两个角频率差2倍的正弦曲线组合得到是一个不规则的曲线。

    02-阻尼

    所有的运动都会伴随一些阻力，否则，这个世界将会变得杂乱无序。把管道系统运动的阻力综合在一块，统称为管道系统的阻尼。阻尼大致分为两类：黏性阻尼和库伦阻尼。黏性阻尼是与相关联结构部分的速度成比例的阻力，库伦阻尼与结构接触面摩擦力成比例。振动方程里面的阻尼是指黏性阻尼。尽管如此，在实际应用中，阻尼系数其实包含一部分的库伦阻尼。设计阻尼系数值来源基于经验数据，阻尼对管道系统的影响是两种阻尼综合的作用，并非某单一阻尼。

    设计阻尼值通常特指临界阻尼的百分比。从前面的计算中我们可以清楚的看到，设计阻尼对结构的响应影响是很大的。所以正确选择设计阻尼值是一个结构系统设计的关键点之一，对管道系统设计来说也一样。

    管道系统的阻尼主要来源于下面这些因素的影响：管道材料，尺寸，保温，介质，支架形式等。它也与材料的应力水平和管道的变形程度相关。也就是说，得到精确的阻尼值是相当困难的。如果没有精确的数据，工程上会采用较保守的阻尼值，但是，过分的保守又会导致不切实际的设计。

    上世纪70年代，是核电站建设的繁荣期，将管道系统动态分析纳入常规设计内容就是从这个时候开始的。根据Newmark算法给的应力水平建议值来确定整个管道系统要取的阻尼值。这个方法在1973年美国核管理委员会管理指南的创刊号上面首次被确定采用。并给出了管道系统阻尼值取值方法，如下表。

    很多核电站都是基于这种方法设计的。为保证核电站在指定的地震作用下能安全运行，每个核电站至少采用了1000个阻尼器来保证管道系统拥有足够的阻尼。当然这么多的阻尼器不但增加了核电站的建造成本，也延长了标准的停机维护时间。为保证阻尼器正常的发挥作用，每次停机维护期，都要对阻尼器进行逐个的检测和测试。因为大量的阻尼器都安装在狭小的空间里，过道拥挤，不便操作，其维护时间比填料和其它维护时间还要长。所以，在满足需求前提下尽可能的减少阻尼器的数量就成为设计很重要部分。

    减少阻尼的数量有几种方法。第一种是采用更为精确的计算方法，比如时间历程分析采用多支承激励地震响应谱法代替包络谱分析法。第二种方法是通过优化管道系统，用尽可能多的刚性支架代替阻尼器。另一种是减少设计规范的限制，因为只要涉及到规范的地方，应力水平基本上都会被限制的很死，没有太大的调整空间。换句话说，阻尼值的并没有得到很好的定义，依然具有很大的优化空间。

    增加设计阻尼的最有效方式就是直接实验。因为阻尼值涉及到百万美元的建造成本，因此优化阻尼的方法是大家一直探寻的。比如日本，他们特别热衷于直接实验的方法来解决阻尼的问题，他们对管道系统采用的阻尼比仅为0.5%。美国和其它国家做了很多这方面的实验，得到了大量有用的数据。美国压力容器研究委员会WRC分别于1984年和1986年发布了这方面的增补内容，美国核工业协会基于这些增补修订了管理指南并最终于2007年发布。修订后的值在上面的表中可以看到。